Biochar first came into broad public awareness through the example of the Amazon, where the hypothesis is that Amazonian inhabitants added biochar along with other organic and household wastes over centuries to modify the surface soil horizon into a highly productive and fertile soil called Terra Preta, which is in direct contrast to the typical weathered Oxisol soils in close proximity. Biochar is exciting to many people because of its role in such soil-building processes. Those who have used biochar for several years may obtain tangible positive results, but they may not have solid concepts and theories about how it works. Biochar is a heterogeneous and chemically complex material and its actions in soil are difficult to tease apart and explain mechanistically.
In this article, I will describe some of the most robust theories of how biochar works in soils, explaining these mechanisms in common language. I begin by examining the role of soil carbon in general and then drill down to a "nano-scale view" looking at the chemical, electrical, physical and biological processes that biochar seems to stimulate. While there are now multi-year field studies that show the impact of biochar on different crops, it is difficult to draw broad conclusions from these studies since they use different kinds of biochar in different types of soil with different crops. To really understand biochar, it is perhaps more useful to look first at some general functions and properties of biochar. I look then at its behavior in compost, which is like an experimental incubator where many soil processes are accelerated. I review a few recent studies of biochar in compost in order to tentatively explain what biochar actually does when it comes into contact with organic matter and minerals – the basic constituents of soils.
The Role of Carbon in Soil
To understand biochar, we must first appreciate the role of soil carbon. Soil carbon comes in many forms. There are two main pools of carbon: organic and inorganic. Organic forms can be further divided into "recalcitrant carbon" or resistant to decay, like humus, and "labile carbon," where the carbon is both bioavailable (in the form of easily degraded compounds such as oils, sugars and alcohols) and physically accessible to microbes (not bound up with minerals). The organic carbon pool includes both the living bodies and the dead, decomposing bodies of bacteria, fungi, insects and worms, along with plant debris and manure. Inorganic carbon consists of carbonate ions, which are typically found as salts like calcium carbonate, and dolomite minerals, mostly in the form of rocks and sand. However, the main distinction of the inorganic carbon pool is that it does not fundamentally provide microbes with energy for feeding the soil building reactions.
The evolution of soil shows how the soil building process works. Before photosynthetic bacteria transformed Earth's atmosphere by filling it with oxygen, soil was nothing more than a mineral mixture of anoxic green clay. After oxygen entered the atmosphere, minerals started reacting with the oxygen, and red iron oxides appeared in the soil. Good organic, rich, productive soils developed slowly only after algae and arthropods crawled from the sea to dry land and plants took root (Fortey, 1999). Life colonized land and began shedding its wasted, used up and discarded parts onto the earth where they formed a carbon-rich banquet that allowed new life to feed and grow, using photosynthesis to pump ever more energy into the system.
Soil building is the product of a self-reinforcing, positive feedback loop. But soil decline is also a self-reinforcing loop that can result in catastrophic soil loss. Most forms of agriculture tend to deplete soil carbon by reducing the amount of natural organic inputs from leaf and fruit fall as well as from woody debris as it is found in native ecosystems. However, modern, chemically-based agriculture depletes soil carbon much more drastically. Nitrogen fertilizers combined with tillage accelerate microbial respiration, burning up soil carbon faster than it is replaced. Due to the loss of organic carbon reservoirs, many soils have become nearly lifeless substrates that must be continually fed with irrigation water, mineral nutrients and pesticides to produce a crop. Although productive in the short term, this practice is not sustainable. Soil scientist Rattan Lal (2010) estimated that "Most agricultural soils have lost 25% to 75% of their original soil organic carbon (SOC) pool."
Is it possible that biochar can substitute for some of this missing soil carbon? Some of the most productive and resilient soils in the world contain significant quantities of "natural" biochar. Nature makes megatons of biochar in the process of naturally occurring wildfires in forests (Goldberg, 1985). Prairie fires can also generate a lot of biochar (Old, 1965). Tall grasses burn quick and hot, however, close to the ground where the roots start, air is excluded so the base of the grasses will pyrolyze and not burn. This kind of natural charcoal is present in some of the most valuable agricultural soils in the world: the carbon-rich Chernozems of the Russian steppe and the Mollisols of the US Midwestern prairie states (Skjemstad et al, 2002; Glaser & Amelung, 2003). Recently, scientists (Mao et al, 2012) have looked more closely at the Mollisols, and found that they contain charcoal that is "structurally comparable to char in the Terra Preta soils and much more abundant than previously thought (40–50% of organic C)."
Biochar - the Electric Carbon Sponge
Carbon comes in many forms, and the terminology used to describe it can be confusing. Organic carbon refers to the carbon in compounds that are found in living or once-living things. Those compounds include hydrogen and oxygen in the form of hydrocarbons and carbohydrates. Inorganic carbon includes the carbonates such as limestone, and even though some life forms use carbonates to make their shells or skeletons, these compounds are still termed "inorganic". Mineral carbon refers to carbon solids like diamond and graphite as well as the gases of carbon (CO2, CO and many others). Also, there are numerous ways a carbon atom can be arranged in a solid which leads to different physical structures, which are called allotropes. Allotropes of mineral carbon, include diamond, graphite, graphene, buckyballs and carbon nanotubes (Figure 1).
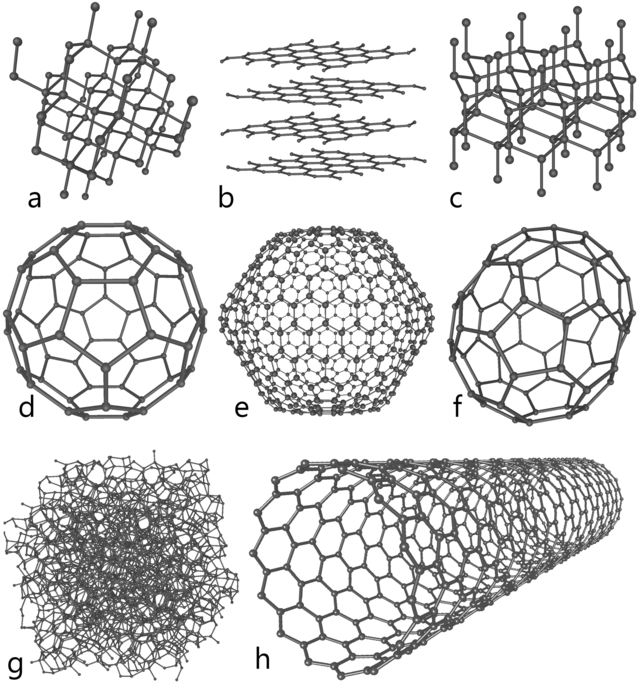
Figure 1. Eight allotropes of carbon: a) Diamond, b) Graphite, c) Lonsdaleite, d) C60 (Buckminsterfullerene or buckyball), e) C540, f) C70, g) Amorphous carbon, and h) single-walled carbon nanotube or buckytube. Design created by From: en.wikipedia.org—Allotropes_of_carbon
So what is biochar then? Organic or mineral carbon? Actually biochar is a mixture of both, depending on the conditions of formation. But let’s first look at how biochar is produced. Biochar is made by heating biomass under the exclusion of air. This process is called pyrolysis, which includes the drying of the biomass and the subsequent release of flammable vapors. Technically this can be done by many different methods. Some methods use a retort, which is a closed vessel that is externally heated. Heat is transferred through the metal vessel and vapors pass out of a vent where they can be burned and help heat the retort. Gasification is another method that supplies enough air to burn the vapors, but prevents the complete combustion of the biomass material by excluding air from the charcoal zone, thus preserving the biochar. Many other methods of charcoal making exist that range from simple pit kilns to multi-million dollar machines producing energy in gas or liquid form from the vapors.
The resulting charcoal resembles a blackened, shrunken version of the original biomass. But it now has very little hydrogen and oxygen. Microscopically, it inherits much of the structure of the original biomass. The only difference is the material now has been converted from lignin, cellulose and hemicellulose to many of the allotropes of carbon shown above (Figure 1); however, you will not find any diamonds in biochar! What you will find is a collection of disjointed graphite crystals based on hexagonally-shaped carbon rings, with some leftover hydrogen and oxygen attached, along with minerals (ash) that were in the original feedstock. These hexagonal carbon compounds are fused carbon rings. Fused carbon rings are also called "aromatic" carbon, (another confusing chemistry term - it does not mean that the compound has a strong aroma, although some of them, like benzene, do). They are very stable and it takes microbes a long time to degrade them. The more you heat the biomass, the more of these fused carbon rings are created (Keiluweit et al, 2010). The rings hook up with each other to form layers and layers of discontinuous, rumpled sheets - the graphite crystals. A single layer sheet is called graphene. Biochar's jumble of carbon crystallites is an important source of its porosity – imagine all the tiny spaces in the wrinkles between sheets.
Biochar starts out as organic and becomes more mineral-like with heating. This mineral transformation creates the skeletal structure that looks like a carbon sponge (Figure 2). While the mineral, fused–carbon ring structure is hardly biodegradable, the recondensed vapors that can be found in the biochar pores and on its surfaces are less aromatic and more biodegradable and can thus be considered organic phases of the biochar.
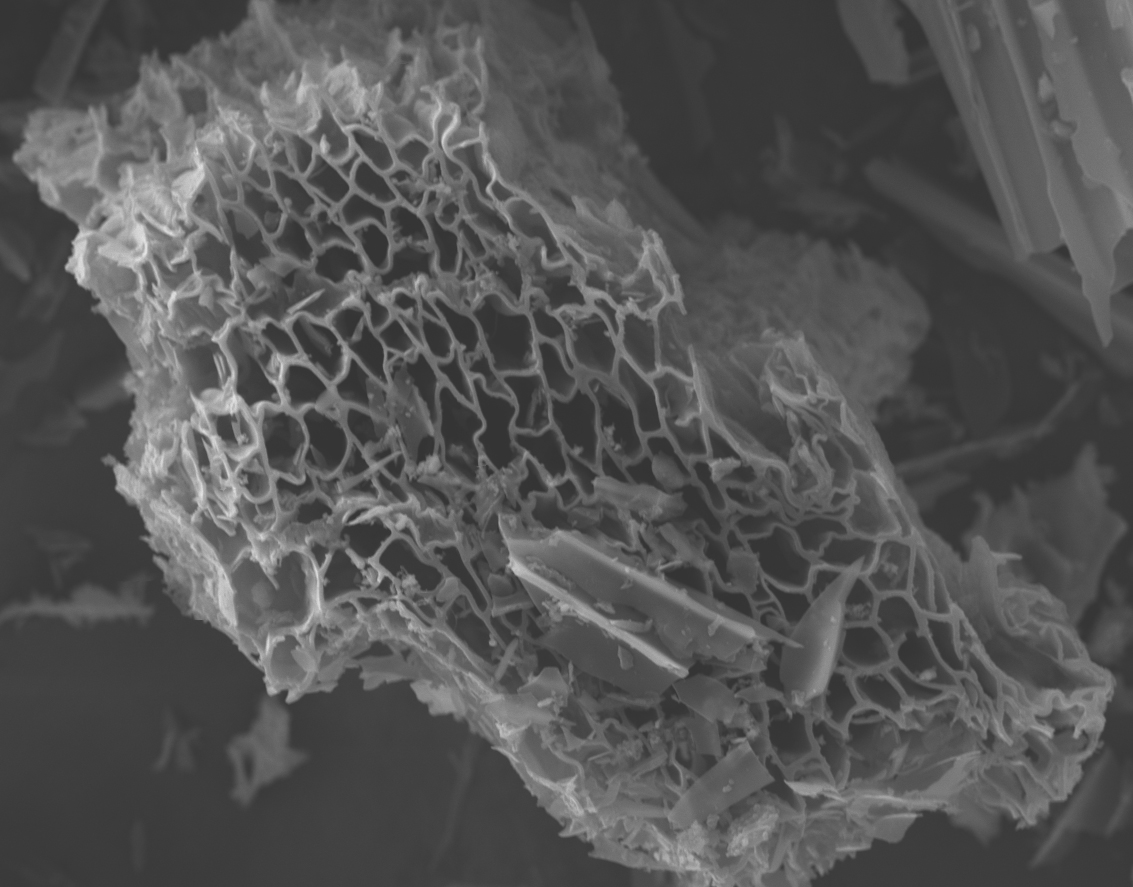
Figure 2. The skeletal structure of biochar looks like a carbon sponge.
The fused carbon rings are also responsible for the electrical activation of the biochar carbon sponge. Fused carbon rings form a special bond with each other that allows electrons to move around the molecule (Figure 3) producing electrical properties like those that are found in engineered carbon materials such as graphene sheets and carbon nanotubes. Depending on the pyrolysis temperature and resulting arrangement of atoms, biochar can be an insulator, a semi-conductor or a conductor of electricity. Electrically active fused carbon rings also support “redox” or oxidation and reduction reactions that are important to soil biochemistry, by acting as both a source and sink of electrons. In soils, microorganisms use aromatic carbon both as an electron donor and as an electron acceptor during metabolic chemical reactions (Lovley et al, 1996). Biochar seems to not only serve as an electron buffer for redox reactions (Klupfel et al, 2014), but it also helps bacteria swap electrons among themselves, improving their metabolic efficiency as a microbial community (Kappler et al, 2014; Chen et al, 2014).
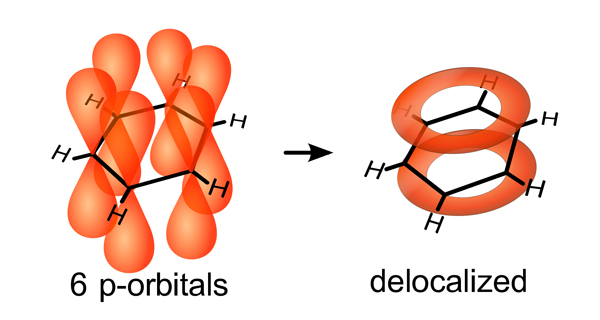
Figure 3. The special bond of fused carbon rings, as exemplified by a benzene molecule. Electrons in the 6 p-orbitals become delocalized around the hexagonal carbon ring. Creative Commons CC-BY-SA: http://en.wikipedia.org/wiki/Conjugated_system
With its pores and its electrical charges, biochar is capable of both absorption and adsorption. Absorption (AB-sorption) is a function of pore volume. The larger pores absorb water, air and soluble nutrients like a normal sponge. Adsorption (AD-sorption) depends on surface area and charge. The surfaces of biochar, both internal and external, adsorb materials by electro-chemical bonds, working like an electric sponge.
Porosity comes in many scales, from the relatively large vascular and cellular structures preserved from the original biomass, to the nano-pores formed by tiny molecular dislocations. The amount of porosity depends mostly on the feedstock material, particle size, and the highest treatment temperature (HTT) (Brewer et al, 2014). Temperature determines how much of the volatiles (hydrogen and oxygen containing compounds) will be driven off and how much pure carbon graphite is formed. Generally, porosity increases the more volatiles are driven off, clearing the pores, although they can re-clog when vapors are incompletely driven off and condense on the forming biochar surfaces. Also, at temperatures approaching 1000 degrees C, pores begin to collapse or melt. For this reason, HTT is a key variable to know when specifying a biochar for a particular purpose. Porosity will also depend on the feedstock, with high ash feedstocks like grass reacting quite differently to heating than low ash feedstocks like wood or bamboo. For wood feedstocks, porosity typically peaks at an HTT of about 750 degrees C (Downie et al, 2009).
When several aromatic carbon rings cling together with some hydrogen on their outer sides they are called polycyclic aromatic hydrocarbons (PAH). These compounds are composed of only carbon and hydrogen (Figure 4). In most cases, the longer they are, the more stable they are. However, 16 (identified by the US EPA) of the PAH molecules are confirmed or suspected to be hazardous to the environment and human health. These PAHs are mostly found in soot and tar and are produced in all sorts of fires or thermal decomposition of biomass and fossil fuels. They are also produced when biochar is made; however, most of them are driven off with the vapors as their boiling point is lower than the usual pyrolysis temperature. If the pyrolysis conditions and the separation of the solid biochar and the vapors are not optimized (like in some gasifiers) the produced chemicals can become a problematic contamination of the biochar and potentially hazardous to the environment and user (Hilber et al, 2012; Hale et al, 2012). For that reason the International Biochar Initiative (IBI, 2012) and the European Biochar Certificate (EBC, 2012) developed analytical protocols for quality biochars, making sure that no hazardous substances enter ecosystems in critical amounts.
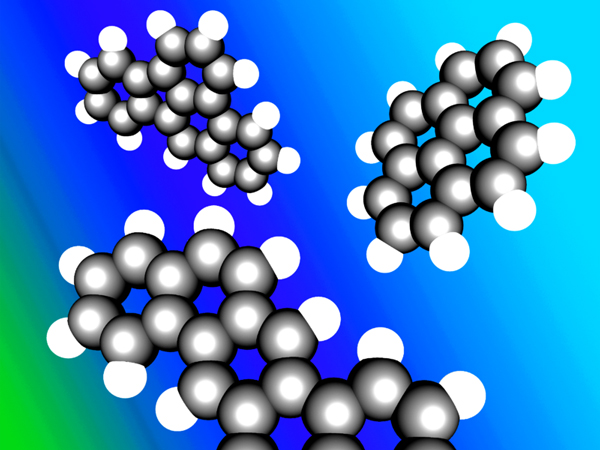
Figure 4. Ball and stick representation of PAH examples. Clockwise from top left: benz(e)acephenanthrylene, pyrene, and dibenz(ah)anthracene. Designed by: Denis Bogdan, Creative Commons CC-BY-SA: https://en.wikipedia.org/wiki/Polycyclic_aromatic_hydrocarbon
Interestingly, biochar is also effective as a PAH adsorbent and could be used to clean up PAH and other substances from soil (Chen & Chen, 2009). IBI and EBC certified biochars, with low measurable concentration of PAH, can potentially reduce the amount of leachable PAHs already existing in soils through adsorption to the biochar. Irrespective of this fact, PAH contents of biochar have to be controlled, as otherwise a good idea can easily turn into its opposite. Problematic in this regard is that PAH analyses are expensive and in most countries not yet available. To test biochar in the absence of sophisticated analysis, you can simply smell it and touch it. If it smells like anything don’t use it. Rub a bit on your skin. If it feels greasy and requires soap or detergent to remove, don’t use it without further testing. This easy field test works rather well because PAHs only stick on a biochar in considerable amounts if condensates from the vapor phase have been adsorbed during the production process - in that case many other compounds leaving an odor or taste would also stick to biochar surfaces.
A Well-Aged Cheese
Biochar is not soil. The electric carbon sponge is only an ingredient in the mineral and organic stew that makes up soil. The dish is usually potluck, composed of whatever the local geology and biology provide. However the Terra Preta soils are different. The fertility of these black, humus-rich soils is many times greater than the surrounding, highly leached red soils. They may have been deliberately created over centuries by people living on densely settled high bluffs along the Amazon River. It is thought that the ingredients included charcoal, ash, food scraps and human excrements, but how they actually combined to form Terra Preta is unknown. Explaining the formation of the Terra Preta is like determining the recipe for a fine Camembert cheese. You can analyze all the ingredients and still have not the faintest idea how to make one if you don’t learn it from the artisans.
One thing that is becoming obvious after a decade of biochar scientific research and the first results from multi-year field trials is that, just like a good cheese, the time dimension is critical. From the moment that biochar is pulled from the kiln, its surfaces begin to oxidize and form new compounds. These changes result in different molecules attached to the surface, called “functional groups,” composed primarily of oxygen, hydrogen and carbon. These functional groups are able to bond with nutrients and minerals, while the fused carbon rings support redox reactions and shuttle electrons around the microbial community attached to biochar surfaces, potentially enhancing microbial metabolism and the cycling of nutrients. The end result of this ferment could be any one of many “terroir”-distinct Terra Preta flavors, depending on what kind of soil, organic matter, minerals, water and life forms come into contact with the biochar, and how long it has to ripen. But, if you sample the cheese before it is mature, it’s just sour milk.
Raw biochar placed in soils before it has a chance to collect a charge of nutrients can actually reduce crop yields because 1) it reduces the availability of plant nutrients by binding and immobilizing them and/or 2) it may add volatile organic compounds (labile carbon) that feed a bloom of microbes that use up nitrogen in the soil, depriving plants. These problems are easily corrected by adding fertilizer to the charcoal application to compensate for this effect. Once the labile carbon fraction is used up, biochar enters a new phase - a deep time dimension where its carbon matrix is stable for hundreds to thousands of years and may become the core of humic substances that crystalize around the fine biochar particles (Kluepfel et al, 2014); at least this is what the existence of ancient fertile black earth soils suggests.
In fact, biochar, whether naturally created or man-made, may be the base of many humic materials found in soils (Hayes, 2013). Very little humus naturally forms in tropical soils, where high temperatures and moisture accelerate microbial decomposition, yet Terra Preta soils have a high content of humus. To understand why, Liang et al (2010) added new organic matter to both a Terra Preta soil and an adjacent, poor natural soil. They found that more of the organic matter was retained as stable humus in the Terra Preta soil. A combination of factors may lead to this result. Biochar surfaces adsorb carbon and retain it in compounds with minerals, supporting at the same time a large microbial community that potentially makes more efficient use of organic debris containing carbon and other nutrients. The existence of this mechanism raises the possibility that Terra Preta soils are thus able to accumulate additional carbon more efficiently than adjacent soils .
If tropical soils need biochar to make humus, what about compost? Well balanced compost, with the optimum C:N ratio, will contain lots of humus. However, if there is not enough stable carbon (from wood, straw or other lignin sources), then the easily degradable sugars, fats and proteins will be completely consumed by microbes leaving very little substrate behind. This is what happens in tropical soils where heat, moisture and high microbial activity will decompose a fallen leaf nearly as soon as it hits the ground, allowing very little soil to form.
A number of studies have demonstrated that biochar has value as an ingredient in compost that can help capture nutrients and form humus. In the next section, we review some of these results and explain why biochar is valuable in compost. The answers will also tell us a lot about how biochar behaves in soil, because compost accelerates many of the processes that occur in healthy soil.
Kickstarting Compost with Biochar
If you look at a list of things biochar is supposed to do in soil, you'll find it is very similar to lists you see for compost. Both biochar and compost are said to provide these benefits, taken from various claims made by biochar and compost manufacturers:
- Improves tilth and reduces soil bulk density
- Increases soil water holding capacity
- Becomes more stable by combining with clay minerals
- Increases cation exchange capacity (CEC - the ability to hold onto and transfer nutrient cations: ammonium, calcium, magnesium, and potassium)
- Improves fertilizer utilization, by reducing leaching from the root zone
- Retains minerals in plant available form
- Supports soil microbial life and biodiversity
- Helps plants resist diseases and pathogens
- Helps plants grow better in high salt situations
- Adds humus carbon to the soil carbon pool, reducing the atmospheric carbon pool
If compost really can do all these things, why do we need biochar? The answer is twofold:
First, unlike biochar, compost is quickly broken down by microbial action in soil over months to at most, decades, depending primarily on climate. Biochar lasts at least ten times longer in most soils. Recently, I called a California agriculture extension agent with a question about adding compost to fields to improve water holding capacity. I was told that because of the hot climate, at least two applications a year are needed to maintain enough soil organic matter to make a difference in water holding capacity. Aside from the expense of applying that much compost, there is simply not enough compost available to support such large application rates.
Second, biochar has important synergistic effects when added to compost. Researchers find that biochar makes faster, more nutrient rich, more biologically diverse and more humified, stable compost. Below, I examine several of the most important biochar effects and summarize some recent research results.
1. Biochar keeps compost moist and aerated, promoting increased biological activity.
The composting process is governed by various physical parameters that are subject to alteration by the addition of biochar materials as bulking agents. Some of the parameters that most affect compost are: aeration, moisture content, temperature, bulk density, pH, electron buffering and the sorptive capacity of bulking agents. Water and air are both held in biochar pore spaces and voids, and the spaces between particles. Moisture is also the vehicle for bringing dissolved organic carbon, nitrogen and other plant nutritive compounds into contact with biochar surfaces where they can be captured. Biochar’s stable carbon matrix accepts electrons from decomposing organic compounds, buffering electric charges that might otherwise impair microbial activity and be responsible for the production of greenhouse gases like methane and hydrogen sulfides.
All these properties of biochar promote microbial activity in compost. For instance, Steiner et al (2011) tested 5% and 20% additions of pine chip biochar to poultry litter compost, and found that the addition of 20% biochar caused microbial respiration (measured as CO2 emissions) to peak earlier and at a higher level than either the 5% or 0% biochar treatments.
2. Biochar increases nitrogen retention
When nitrogen-containing biomass materials decay, they can release large amounts of ammonia. Ammonium (NH4+) is the aqueous ion of ammonia. Ammonium is generated by microbial processes and nutrient cascades that convert nitrogen from organic forms found mainly in proteins and nucleic acids into mineral forms (ammonium, nitrate and nitrite) that can intermittently be converted by nitrifying and denitrifying microbes to gaseous emissions that include volatile ammonia gas (NH3), nitrogen gas (N2), nitrous oxide (N2O) and other reactive nitrogen gases (amines and indoles). At neutral pH, the aqueous ammonium (NH4+) and the gaseous ammonia (NH3) are in equilibrium. Higher pH forces more of the aqueous ammonium into the gas phase that can escape to the atmosphere.
Numerous studies have shown that biochar is effective at retaining nitrogen in soils (Steiner et al, 2008; Clough et al, 2013). Several studies have also shown that biochar enhances nitrogen retention in compost, reducing emissions of ammonia and increasing total nitrogen retention by as much as 65% (Steiner et al, 2010; Chen et al, 2010; Huang et al, 2014). The ammonia retention ability of biochar can actually improve during the composting process. Adding 9% bamboo charcoal to sewage sludge compost, Hua et al (2009) tested sorption of ammonia on biochar during composting and found that while ammonia retention was correlated with saturation of binding sites in fresh bamboo biochar, this did not hold for composted bamboo biochar. During composting the biochar is subjected to an accelerated aging process. That means that biochar surfaces get oxidized and enriched by carboxylic (acid) functional groups. The latter more than doubled at the end of the composting period, improving the capacity to exchange cations like ammonia.
3. Biochar improves compost maturity and humic content
Several studies have looked at effects of biochar on the timing and results of compost maturation and found that adding biochar to compost reduced the amount of dissolved organic carbon (labile carbon) in mature compost while increasing the fraction of stable humic materials (stable carbon). Following the addition of 2% biochar to compost, Jindo et al (2012) recorded a 10% increase in carbon captured by humic substance extraction and a 30% decrease of water-soluble, easily degradable carbon. They also found an increase of fungal species diversity in the mature biochar compost as compared to the control and proposed that these fungi were responsible for the increased humification. Another study by Zhang et al (2013) found that sewage sludge composted with wood biochar had up to 30% more humic substances than the control.
4. Biochar compost improves plant growth
Biochar seems to improve the composting process, but how do plants like those biochar-composts? Several researchers have experimented with various combinations of compost and biochar added as separate amendments (Fisher & Glaser, 2012; Liu et al, 2012). These studies found improved plant growth response when biochar was added to soil along with compost. A 2013 study in Germany looked instead at biochar composted together with other materials. Schulz, et al (2013) tested six different amounts of biochar in compost, from 0 to 50% by weight, and also three different application rates of each compost type. Using oats in greenhouse pots on two different substrates (sandy soil and loamy soil), they found that plant growth increased with increasing application rates of each type of biochar compost, which is not surprising since the amount of deliverable nutrients was increased, at least by the compost fraction. However they also discovered that plant growth was increased as the amount of biochar in the compost increased. The biochar may either have improved nutrient retention during the composting process with subsequent enhancement of nutrient delivery to plants, or it promoted plant growth through some other mechanism. However, the researchers confirmed that synergistic effects can be achieved by adding biochar to composts.
How could we put biochar to work in soils?
One of the basic principles of good compost production is that the wider the variety of materials you use, the better the compost. Bruno Glaser and his colleagues, who have studied both the Terra Preta soils and biochar in compost, have proposed the modern material flow management scheme diagramed below (Figure 5) for producing high quality compost with maximum carbon sequestration and nutrient balance to help meet the growing need for replenishing carbon, nutrients and beneficial microbes in agricultural soils (Fischer & Glaser, 2012).
This ideal biochar compost system is based on a speculative reconstruction of the Terra Preta soils. According to this model, these areas began as garbage dumps where accumulation of food wastes, ashes and manure were deposited. However, as populations grew, it is possible that they began to realize that the waste sites were developing into very fertile and productive areas. They may have begun to deliberately manage the material flows of plant biomass, mammal and fish bones, ash, biochar, and human excreta that likely resulted in the Terra Preta soils we see today.
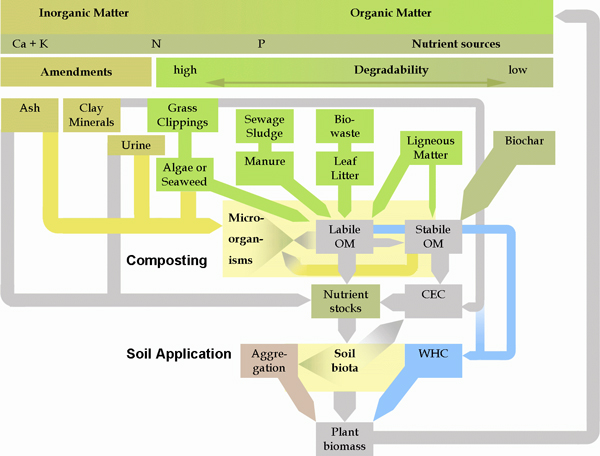
Figure 5. Sustainable management of natural resources by combining biochar with organic and inorganic wastes in compost processing (reproduced from Fischer & Glaser, 2012). OM stands for “organic matter,” CEC stands for “cation exchange capacity” and WHC stands for “water holding capacity.”
For maximum conservation of resources, it is important to remember another principle: use the less degradable carbon sources like biochar to help preserve the more easily degradable but nutrient-laden sources like manure and food waste. I believe there is much exciting work ahead to determine optimum recipes for biochar-based organic composts and ferments, exploring the effects of different kinds of biochar in combination with other compost ingredients.
From past and on-going research, we realize that biochar has numerous possible mechanisms for its action in soils that can occur on a variety of different scales. But if the results from recent biochar compost research prove to be consistent, we now have the beginnings of a recipe book for biochar-enhanced super compost that can kickstart the process of returning carbon to soils today. Our industrial legacy has left us with a rapidly deteriorating climate, and soils that are dying and eroding. Biochar, as a form of recalcitrant carbon, may be just the medicine that degraded and unproductive soils need.
Please download the list of references here
What is it worth for you that this article exists? All of our articles are open source, based on experience and scientific research, reviewed by renowned scientists, independent and free from ads. Please help finance our work with a subscription or a donation to the Biochar Journal. subscribe here


the single best article about biochar I've ever read in over 8 years
tHE BIOCHAR JOURNAL's Kelpie Willson has written the single best article I've ever read in over 8 years of research concerning; How Biochar Works in Soil. She covers it all; Nano-Structure to Electron Transfer to both Ad & Absorption, Organic Vs. Inorganic Carbon, using Fermenting Analogies, covering Composting Synergies, Humus & Chemistry. One of her many citations new to me demonstrate that 400-700 °C Chars show the highest capacities to accept and donate electrons. These are Temperature ranges achieved in open draft & TLUD production methods. *Redox Properties of Plant Biomass - Derived Black Carbon (Biochar).* Environmental Science & Technology, Klüpfel, L., Keiluweit, M., Kleber, M., & Sander, M. (2014) http://www.ncbi.nlm.nih.gov/pubmed/24749810